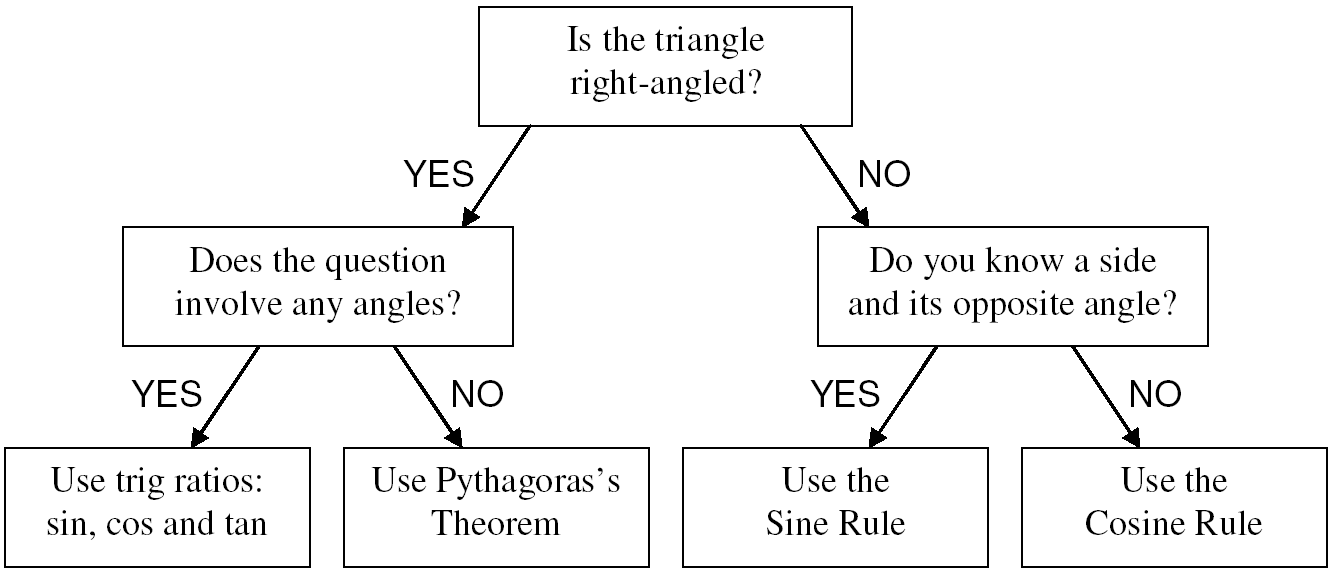
Cosine Rule

For finding sides: $$a^2 = b^2 + c^2 - 2bc \cos(A)$$ and for finding angles: $$\cos(A) = \frac{b^2 + c^2 - a^2}{2bc}$$ $$A = \cos^{-1}\left(\frac{b^2 + c^2 - a^2}{2bc}\right)$$

Sine Rule

$$\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{a}{\sin(B)} $$ or $$\frac{\sin(A)}{a} = \frac{\sin(B)}{b} = \frac{\sin(B)}{a} $$ Both can be used

Pythagoras + Trigonometry Ratios

Don't forget these! RIGHT ANGLES ONLY $$h^2 = a^2 + b^2$$ and $$\sin(\theta) = \frac{\text{opp}}{\text{hyp}}\qquad \cos(\theta) = \frac{\text{adj}}{\text{hyp}}\qquad \tan(\theta) = \frac{\text{opp}}{\text{adj}}$$ $$\theta = \sin^{-1}\left(\frac{\text{opp}}{\text{hyp}}\right)\qquad \theta = \cos^{-1}\left(\frac{\text{adj}}{\text{hyp}}\right)\qquad \theta = \tan^{-1}\left(\frac{\text{opp}}{\text{adj}}\right)$$